This is part of a series of posts.
- KarperScore is born!
- KarperScore Redux
This article refers to deprecated software and methods. It is presented here for archival purposes only.
In my earlier post, I provided a quick-n-dirty solution to the problem of devising a superior system of scoring songs played in Amarok. After giving the problem some thought, I have come up with a different approach.
The score of a song represents the computer’s best guess of how much you, the user, likes a certain song. Unlike the rating, the score requires little user input. Of course, if the rating is provided, the computer can predict the score a lot more reliably. In any case, the parameters that the computer can track and use in determining the score of a song are as follows:
- the previous/current score of the song (
prevscore: 0-100) - the rating of the song (
rating: 0-10) - the play count of the song (
playcount: 0-inf) - the percentage of the song listened to now (
percentage: 0-100)
How important are each of these parameters in judging the score of the song?
The prevscore is our current best guess and needs to be refined.
The rating is the absolute indication of how much you like the song.
But over time, it is likely to be obsolete—the user may grow to like or dislike the song over time and the rating might not be relevant over time.
The playcount indicates how obsolete the user’s rating is likely to be.
If the playcount is high, it is possible that despite a low rating, the user does indeed like the song quite a bit.
Finally, the percentage of the song that was just played is an important, though limited parameter in our decision—it’s altogether likely that the user had to stop the song because of an important call, for example.
In what follows, the code is provided in the Ruby programming language.
Let’s start with the prevscore.
It’s our initial best guess of how much the user likes the song.
If the song was never played before, the score would be returned as a default value, 0.
Just to make sure it is so, the first if statement sets this:
if ( playcount <= 0 )
prevscore = 0We need to next consider the rating of the song.
Again, it’s possible that the rating is not present for the song.
In that case, the computer must make a decision.
Conservatively, I start it off at a rating of 5 - that’s two and a half stars.
if ( rating <= 0 )
rating = 5The choice of the ‘<=’ logical operator is inspired by the default Amarok scoring script. Now, we are ready to make our first guess at the new score.
guess1 = ( 5 * rating ) + ( prevscore / 2 )In other words, the rating and the prevscore are averaged.
Let’s examine the stability of this guess.
It’s immediately clear that this algorithm will always approach the condition prevscore = 10*rating.
This was the basis of my first solution.
To improve our guess, the playcount must be considered.
If the playcount is high, it should reasonably imply a higher score.
This guess must be bounded by the user’s rating and the maximum, 100.
A good candidate function to execute this gradual move from the user’s rating to 100 is the exponential decay function.
guess2 = guess1 + ( 100 - guess1 ) * ( 1 - Math.exp( -playcount / 100 ) )The playcount is divided by 100 to make the typically fast exponential decay a hundred times slower.
Over hundreds of plays, the song’s score will now drift away from the user’s rating towards 100.
Finally, the percentage variable is brought in.
This variable has the potential to wreck havoc on any algorithm—indeed it was the primary reason why I embarked on this endeavor in the first place.
On the other hand, we must recognize the potential to introduce a little ambiguity in the scoring process.
It does become boring to stare at a score forever pinned at 99.
A little disturbance in the Force might be a good thing from time to time. :)
In order to contain the damage this variable can do, I let it have control of 10% of the current best guess — guess2.
If the song is immediately skipped, the score will drop to 90% of its current value.
guess3 = guess2 * ( 0.9 + 0.1 * percentage / 100 )A final look at the stability of this algorithm is warranted.
Initially, the prevscore will tend towards the rating, barring the effect of sub-100 percentage values.
As the playcount increases into the hundreds, the exponential function will invariably take over and take the score towards 100.
The percentage can disrupt this from time to time, but the score will always return back towards 100.
This, then is the thought process that went into the design of KarperScore 2.0.
It’s currently in testing.
I’ll release it as soon as I’m sure it’s working as I expect it to.
The future improvements to this code should let the user decide parameters like the default rating, or the relative importance of the percentage variable to the score, etc.
Update
What a difference the class of the variable makes!
Many of the variables above, such as playcount were initialized as integers and the exponential function likes floats!
So, the score was jumping all over the place.
Now, all variables have been initialized as floats and that solved all the bugs I noticed with the script during testing.
The script is ready for general release as far as I can tell, but a couple of days more of testing the code is always a good idea.
Update 2
KarperScore has been working so well for me over the past couple of weeks that I’ve been using it that I wish I could reset all my playcounts and scores, to start all scores fresh.
I need to ask someone on the Amarok IRC channel (#amarok on irc.freenode.net) if that’s possible at all…
I did a simulation of how the score of a song varies over one hundred plays, assuming that the user sets a (constant) rating when the song is listened to for the first time.
That’s why the scores always start at 25 for each of the three cases - no rating (blue), full rating (red) and minimum rating (green).
I also assumed that the user listened to the song in its entirety everytime it’s played (percentage = 100).
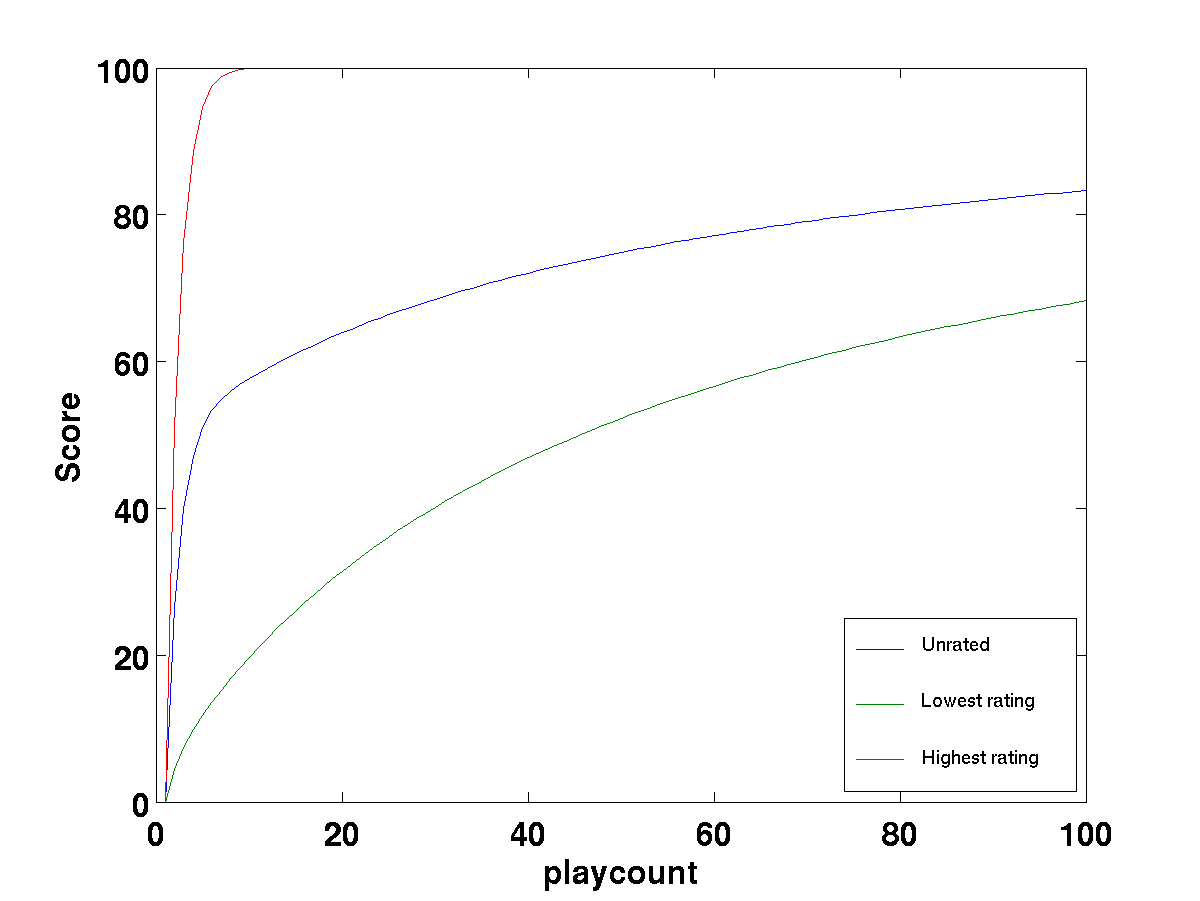
Clearly, for an unrated song, the score approaches 100 leisurely, making it to about 88 after the user listened to the song for the hundredth time.
It’s a good guess of how much the user might like the song after so many plays.
If the rating is specified, the score tends faster or slower than this.
The fastest rise is for the five-star rated songs—the score passes 90 if the song is played just four times.
The lowest minimum rating possible is a half-star.
Note how the score approaches the rating over the first few plays and then slowly climbs as the song collects more playcounts.
When played for the hundredth time, the score reaches about 80.